例题1
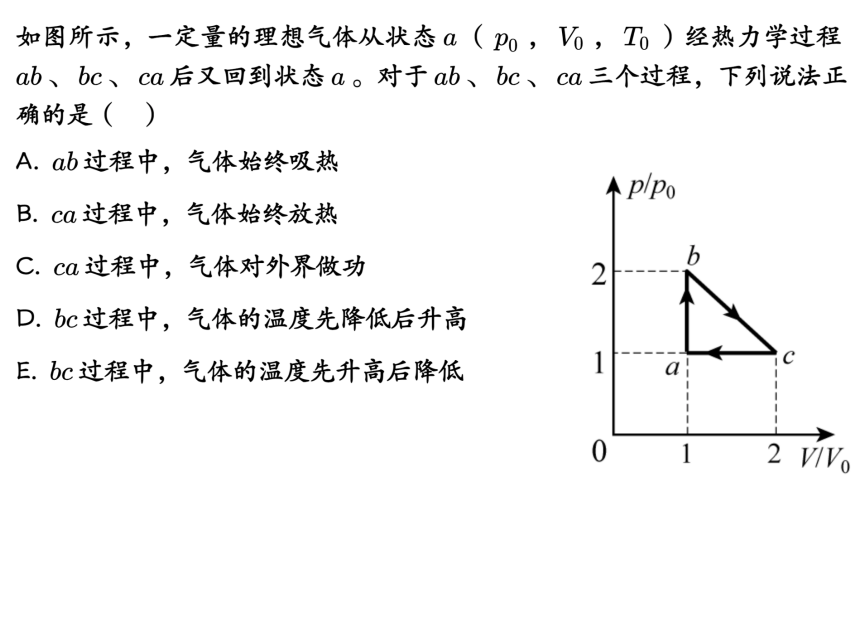
- 答案
- 知识点:热力学第一定律(重点)
- 补充:
- \(F.c \rightarrow a \rightarrow b \rightarrow c\),外界对气体做负功,气体对外界做正功,气体从外界吸热(吸热/放热)
- \(G.c \rightarrow b \rightarrow a \rightarrow c\),外界对气体做正功,气体对外界做负功,气体从外界放热(吸热/放热)
- 解题方法:
- 看上面一段的气体变化过程
练习题1



- 答案:AC、CD、BC
摩尔类计算问题
- \(N_A\)就是\(1mol\)对应的个数
- \(N_A =\)\(6.02 \times 10^{23}mol^{-1}\)☀️
- 题型特征:涉及到摩尔质量、摩尔体积和阿伏伽德罗常数
-

-
- 分子占据体积
- 固体、液体:分子间隙很小,分子占据体积就是分子本身的体积
- 气体:分子占据的体积不是分子本身体积!
分子热运动
- 物质分子都在永不停息的做无规则的运动
- 分子:只有分子才能做热运动,宏观物体不行
- 永不停息:只有达到绝对零度热运动才会停止,也是热力学第三定律
- 无规则:速度的大小、方向没有任何规律
- 热运动=无规则热运动
扩散现象
- 不同物质分子能够彼此进入的现象
- 原因:分子热运动。是分子做热运动的直接证据之一
- 液体、气体、固体中都能发生扩散现象
- 影响因素:温度。温度越高,扩散越快
布朗运动
- 布朗运动:悬浮在液体/气体中的微粒or颗粒所做的无规则运动
- 根本原因:液体或气体分子对微粒的无规则撞击
- 意义:间接反映了液体或气体分子的无规则热运动
- 影响因素:温度越高越显著。微粒越小越显著
扩散现象VS布朗运动
| 扩散现象 | 布朗运动 | |
|---|---|---|
| 运动粒子 | 物质 分子 (液体、气体、固体 ) |
微粒或颗粒 (液体、气体 ) |
| 宏观or微观 | 微观 |
宏观 |
| 证明分子热运动 | 直接证据 | 间接证据, 液体或气体分子 对微粒的无规则撞击 |
| 影响因素 | 温度越高,扩散越快 |
温度 越高越显著。微粒 越小越显著 |
分子运动速率
- 温度越高\(\leftrightarrow\)物质内部的分子热运动越剧烈
- 围成面积之和,都为1
- 温度越高,峰值越靠右
- 温度越高,所有分子速率都更快(对or错):错
- 温度越高,图形矮胖
- 温度越低,图形高瘦
分子作用力
- 分子之间同时存在引力和斥力
- 分子作用力是引力和斥力的合力
- 引力:随着分子间距的减小而增大
- 斥力:随着分子间距的减小而增大
- 分子作用力
-
- :引力\(=\)斥力,合力为0,平衡位置☀️\(r=r_0\)
- :斥力\(\gt\)引力,合力是斥力☀️\(r\lt r_0\)
- :引力\(\lt\)斥力,合力是引力☀️\(r\gt r_0\)
- :分子作用力可忽略☀️\(r \gt 10r_0\)
- 分子作用力随距离增加先变小再反向变大再变小
分子动能
- 分子总动能:物体内所有分子动能之和
- 分子平均动能:物体内所有分子动能的平均值
- 温度是衡量分子平均动能的标志
- 温度越高,平均分子动能越大。但不一定每个分子的动能都增大
- 分子动能不是动能,与机械运动的速度大小无关!
- 判断:
-
- 物体速度越快,温度越高(错)
- 可以用公式\(E_k=\frac{1}{2}mv^2\),来计算分子动能(错)
- 物体速度越快,温度越高(
分子势能
- 分子作用力对应分子势能
- 仅有分子作用力做功:
-
- 分子作用力做正功,动能增加,分子势能减小
- 分子作用力做负功,动能减小,分子势能增加
- 分子作用力做正功,动能
- 分子作用力和分子势能转换关注\(r_0\),它是分子作用力图像的☀️零点,是分子势能图像的最低点
- 分子作用力是矢量,正负只表示方向,比较大小只能看绝对值
- 分子势能是标量,正负用于大小比较
分子作用力和分子势能转换图

内能
- 一般物体:内能=总分子势能+总分子动能
- 影响因素:温度、质量、体积、物态(固、液、气)
- 理想气体:分子间的间距足够大,可以被任意压缩
- 理想气体因为分子间的间距足够大,所以分子势能为零
- 高中物理中如果不特殊说明,默认气体就是理想气体
- 气体的温度变化 = 内能变化 = 气体平均分子动能变化
- 只有分子力做功,分子动能和分子势能相互转化,内能守恒
- 只有分子力做功,分子动能+分子势能=常数
- 只有分子力做功,若分子势能最大,则分子动能最小,若分子势能最小,则分子动能最大
热力学第一定律(重点)
- 公式:\(\Delta\boldsymbol{U}=\boldsymbol{Q}+\boldsymbol{W}\)☀️
- \(\Delta\boldsymbol{U}\):是内能变化量,升温是+(正),降温是-(负)
- \(\boldsymbol{Q}\):是热传递,吸热是+(正),放热是-(负)
- \(\boldsymbol{W}\):是外界对气体做功
- 特别注意是谁对谁做功,公式中的\(\boldsymbol{W}\)专门指的是外界对气体做功
- 外界对气体做功和气体对外界做功正好相反
- 气体体积变大,外界对气体做负功,\(\boldsymbol{W}\)是-(负)
- 气体体积变小,外界对气体做正功,\(\boldsymbol{W}\)是+(正)
- 题型特征:求内能变化,温度变化,吸热,放热的题目就摆公式\(\Delta\boldsymbol{U}=\boldsymbol{Q}+\boldsymbol{W}\)☀️
热力学第二定律
- (1).自发热过程,有方向。方向的确定,参考熵增原理
- (2).能量不能全部转换成有用功,会有损耗
- 下面是补充(了解)
-
- 自发:不需要消耗其他能量、没有能量损失、不需要别人帮忙
- 克劳修斯表述:热量不能自发地从低温物体传到高温物体
- 开尔文表述:不可能从单一热库吸收热量,使之完全变成功,而不产生其他影响
- 凡是现实中存在的现象肯定是不违背热力学任何一个定律的
熵增原理
- 熵用于描述系统的混乱程度
- 熵增原理:一个孤立系统总是自发地向无序方向发展,即熵总是增加的
- 所有自发的热过程都是从有序变为无序
热力学第三定律
- 不可能把物体冷却到绝对零度
- 绝对零度:分子热运动完全停止时的温度,约为-273℃
- 本质:分子热运动永不停息
理想气体
- 分子大小和相互作用力忽略不计,也不计气体分子与器碰撞的动能损失。
- 分子势能为0,内能=分子总动能
- 是一种理想模型
- 高中阶段如无特殊说明,气体=理想气体
温度
- 摄氏温度:单位:摄氏度,符号℃
- 热力学温度:单位:开尔文,符号K,理想气体方程中温度用的是热力学温度
- 以绝对零度为0K
- 摄氏温度转热力学温度用:T=t+273K
理想气体状态方程
- 公式:\(\boldsymbol{\frac{pV}T=nR}\)☀️
- 主要掌握:\(\boldsymbol{p、V、T}\)
- \(\boldsymbol{p}\):压强
- \(\boldsymbol{V}\):体积
- \(\boldsymbol{T}\):温度
- 了解:\(\boldsymbol{n、R}\)
- \(\boldsymbol{n}\):气体的摩尔数,单位:mol
- \(\boldsymbol{R}\):是个常数,不同的气体这个值会不一样
- 封闭气体,变化前后,气体的质量不会变,也就是nR不变
- 假设用数字序号表示不同的状态,1表示变化前,2表示变化后,则有下面
- 公式:\(\boldsymbol{\frac{p_{1} V_{1}}{T_{1}}=\frac{p_{2} V_{2}}{T_{2}}}\)☀️
理想气体微观描述
- 理想气体\(\boldsymbol{T、V、p}\)三个宏观量对应的微观意义
- 温度\(\boldsymbol{T}\):表示气体分子热运动的平均动能。温度越高,气体分子平均动能、平均速率越快
- 体积\(\boldsymbol{V}\):表示气体分子的密集程度。密集程度=气体质量/体积。密集程度与温度无关
- 压强\(\boldsymbol{p}\):器壁单位面积受气体分子的碰撞力。
-
- 压强\(\boldsymbol{p}\):受两个因素的影响:①和②乘起来就是压强
- ①单位时间、单位面积撞击器壁的次数,由体积和温度决定
- ②分子热运动的平均速率,由温度决定
- 压强\(\boldsymbol{p}\):受两个因素的影响:
热力学中常见的已知条件
- 导热良好:\(\Delta\boldsymbol{U}=0\)☀️
- 绝热:\(\boldsymbol{Q}=0\)☀️
- 恒温:\(\Delta\boldsymbol{U}=0\)且\(\boldsymbol{T}\)☀️不变
- 恒压:\(\boldsymbol{P}\)不变
- 气体体积变大:外界对气体做负功,\(\boldsymbol{W}\)< 0
- 气体体积变小:外界对气体做正功,\(\boldsymbol{W}\)> 0
- 注意:外界对气体做功和气体对外界做功是相反的
切线和割线
- 切线斜率:\(k=\frac{\Delta\boldsymbol{y}}{\Delta\boldsymbol{x}}\),相当于数学里面的☀️导数
- 割线斜率:\(k=\frac{\boldsymbol{y}}{\boldsymbol{x}}\)☀️
- 高中物理用到割线斜率的场景:理想气体方程,欧姆定律
- 理想气体图像中:两点的割线斜率如果要相等,一般会有一条过原点的虚线
理想气体图像
- \(\boldsymbol{p}、\boldsymbol{T}\)图像:一般看割线,靠近\(\boldsymbol{T}\),体积大
- \(\boldsymbol{V}、\boldsymbol{T}\)图像:一般看割线,靠近\(\boldsymbol{T}\),压强大
- \(\boldsymbol{p}、\boldsymbol{V}\)图像:一般看围成面积,面积越大,温度越大
热力学大题解题步骤
- 1、列表,有几个封闭气体就列几个表
-
- 格式:
- 1 2 | 1 2
- \(\boldsymbol{p}\) |
- \(\boldsymbol{V}\) |
- \(\boldsymbol{T}\) |
- 2、看不变量
- 3、列方程
-
- 列理想气体方程
- 列活塞受力分析的方程
- 列
压强不变的情况
- 运动过程中,其他力不变,压强不变
充放气问题
- 充入和放掉的气体是同种气体
- 公式:\(\boldsymbol{\frac{pV}T=nR}\)☀️
- 充气:\(\boldsymbol{\frac{p_{1}V_{1}}{T_{1}}}+\boldsymbol{\frac{p_{充}V_{充}}{T_{充}}}=\boldsymbol{\frac{p_{2}V_{2}}{T_{2}}}\)☀️
- 放气:\(\boldsymbol{\frac{p_{1}V_{1}}{T_{1}}}-\boldsymbol{\frac{p_{放}V_{放}}{T_{放}}}=\boldsymbol{\frac{p_{2}V_{2}}{T_{2}}}\)☀️
判断液柱上下表面压强关系——“两线法”
- 公式:\(p_{上}+\rho gh=p_{下}\)☀️
结语
- 热力学这一章,很大概率考察计算题,如果考察计算题,要熟练掌握“热力学大题解题步骤”,要结合高考题去练习
- 也可能考选择题,选择题考察理想气体图像和热力学第一定律